Equivalence in j-space - II
"We often forget the wonder that we felt as children, when the cares of the activities of the "real world" have begun to settle upon our shoulders."
- Roger Penrose
"The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality."
- Hermann Minkowski
Let us say that these observers are earthlings (ObsEarth) and martians (ObsMars). The very first condition that these observers must agree upon is, the Lorentz invariance in their measurements. The Lorentz invariance implies that the space-time interval between two events must be same, as measured by either of these observers. The condition of Lorentz invariance ensures that both observers stay on the same Λ∞-plane.
We know that the discrete measurement space is
a two-state system represented in the complex
space C
(Pauli operators). The
measurements made by the observers are
represented by the points on the complex
plane, also known as the Argand plane. If
all the information available in the unit
circle on a complex plane, can be precisely
measured by the observer, we can safely assume
that Argand plane is complete.
The phrase "If", is loaded
with implications. We
will discuss in detail some
other time,
the assumption that the Argand plane is
complete for a macroscopic observer's
measurements. The Argand plane is
equivalent to the Λ∞-plane in
anharmonic coordinates.
We can map the information available on Argand
plane, onto the surface of a sphere known as
the Riemann sphere.
Essentially we have placed the observer inside
at the center of the Riemann sphere and the
information available in the observer's
universe is contained on the surface of the
Riemann sphere. At a given instant 1,
this information can be transformed over to
another Riemann sphere using Möbius
transformation. The situation is
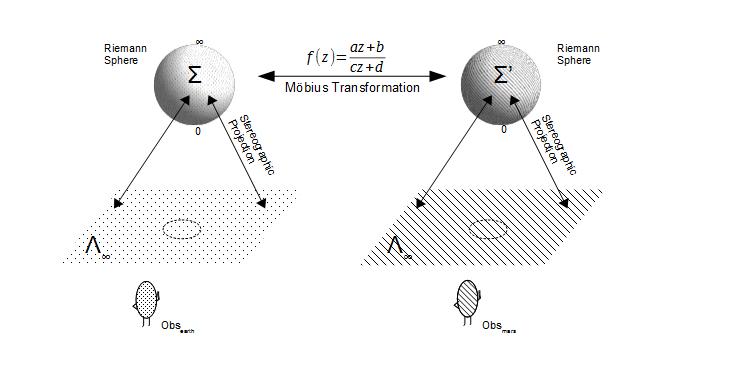
shown in the following figure.
The measurements of Obsearth
are mapped on to Λ∞-plane
on the left. They are then
stereographically projected upon the
corresponding Riemann sphere Σ, which is next
mapped on to another Riemann sphere Σ'
using Möbius
transformation. Now the information from
Σ',
can be extracted and mapped on to Λ∞-plane
on the right, for Obsmars.
The Lorentz invariance
makes sure that Λ∞-planes
are identical for
both observers. However the
interpretation of the information extracted by
Obsmars, will not be
necessarily identical to that by
Obsearth.
The difference may be of the nature that you
say "tomato", I say "tomaato", but it will be
appreciable. This process can be
reversed to transform the description of the
universe per Obsmars,
to the description per Obsearth,
using inverse Möbius
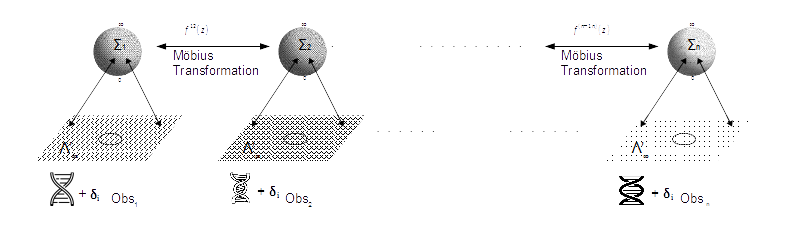
transformation. We can generalize above
process to n observers, where n is a large
number. It will require a minimum of n-1
Möbius transformations for communication
between these observers, if each of these
observers is distinct from others.
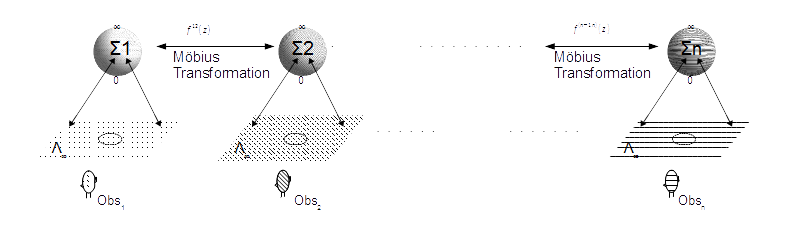
The set of these Möbius transformations and any combination of them will form a group. In j-space, an important feature of these groups is that the required identity element e is the null element {}. In discrete measurement space the null measurement is not possible. The null element essentially is 0j, which has a finite value. We start counting with our abacus using VT Symmetry in j-space, only after determining e, 0j or {}, (i.e. {} + {} + {} + {} +...........).
Now let us up the ante a
bit. Rather than designing a mere
interstellar GPS, we consider the scenario
where life-forms other than those carbon
based, are also in communication. The
situation is as following:
The measurement space will remain discrete and VT symmetry will be required to define the origin or {}. The values of the physical constants will depend on the definition of the identity element e or {}, as determined by VT symmetry. The observers making measurements here, will have to agree on Lorentz invariance to ensure that the Λ'∞-planes are identical, then apply respective Möbius transformations to exchange information.
An important
point to note, is the definition of the observer
making measurement as shown above. In
j-space, every entity is simultaneously an
observer, as well as an object being
measured. The observer and the objects
will stay in the state of measurement, until
the PE1 measurement is completed. We
can not simply lock up the lab and call it a
night until the measurements are
complete. An observer could be a
planet, a galaxy, an atom, or an
unknown. Nevertheless the equivalent
observers, have to follow the
principles behind Lorentz invariance and
Möbius transformations. The
conventional or the deterministic
description of the human observers and their
instruments, as independent of the objects
being measured, is true only for the
inertial frame of reference.
Finally we have a rare treat for ourselves. The Master himself is being interviewed by F. Hund in 1982 at Göttingen, Germany. We are truly not worthy! There is also a set of four lectures on Quantum Mechanics by Prof. Dirac given in 1975 at Christchurch, New Zealand, available on YouTube. An incredible wealth of true knowledge. A must view for non-experts.
___________________1. Again a word of caution here, the definition of "instant" is very important. For example when synchronizing geostationary satellites with the signal from earth in a GPS system, the time resolution of 10-9 seconds may be adequate. However in higher information spaces, resolutions required for the precise definition of an "instant" may not be possible with QED instruments based on the electron-photon interaction only. The limitations of the mechanism behind the measurement apparatus is super-critical in j-space.
***

Previous Blogs:
Sigma-z and I
Spin Matrices
Rationale behind Irrational Numbers
The Ubiquitous z-Axis
Majorana
ZFC Axioms
Set Theory
Nutshell-2014
Knots in j-Space
Supercolliders
Force
Riemann Hypothesis
Andromeda Nebula
Infinite Fulcrum
Cauchy and Gaussian Distributions
Discrete Space, b-Field & Lower Mass Bound
Incompleteness II
The Supersymmetry
The Cat in Box
The Initial State and Symmetries
Incompleteness I
Discrete Measurement Space
The Frog in Well
The Einstein Theory of Relativity
***
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits. This is a human-readable summary of (and not a substitute for) the license.