
| The Origin |

| The Origin |
Home |
SUMMARY: We will discuss the problem of the convergence of measurement axes. We will define the origin and as a consequence of our definition of the origin, the discrete measurement space. 
In the
introduction we spoke about the issue of the
convergence of the coordinate axes. We
were not sure what would the origin mean if we
measured it. Let us elaborate further
upon it. Before we launch into a
discussion we close our eyes and assume that
nothing really exists, no sun, moon, earth,
planets, galaxies, atoms, quarks, nor any
prior knowledge to cloud our thinking.
We allow just one thought in our
consciousness, "An abstract
measurement!" We will develop our
description based on what we can measure
only. And our measurements are not of
transient nature, but have permanency to them
so that we can build upon the previous
measurements.
The simplest coordinate frame we can think of is Cartesian co-ordinates or (x, y, z) coordinates. 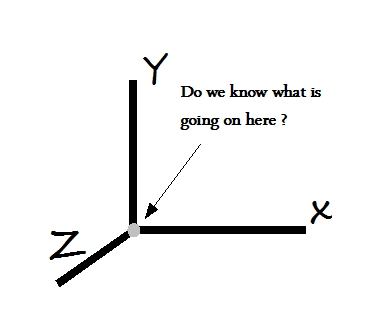 The Cartesian frame
represents how we human perceive the
space. We can
define its properties as follows: The Cartesian frame
represents how we human perceive the
space. We can
define its properties as follows:i) It has an origin which is used as reference for all three axes. ii) It has three axes which behave identically and converge at origin. iii) All three axes are orthogonal to each other i.e. the axes make a 90o angle with each other. Let us consider the definition of origin first. The number systems we use have been classified as natural numbers, integers, real numbers, rational and irrational numbers etc., all of which except natural numbers are counted with respect to an origin defined as “zero”. In the macroscopic world, such determination of origin is sufficient to give an understanding of the events at macroscopic level, make a determination based on observations and arrive at conclusions which determine the course of next event. The determination of “zero” is assumed to be perfect and hence the measurements made with with respect to origin “zero” are considered reliable. However if measurements are made absolute, i.e. the condition is placed that the observer must determine “origin” accurately, then the problem of incomplete resolution is encountered by the observer. What does the origin mean for a measurement? 0.001? 0.000001? or 0.000.....0001? We can continue in this manner until we hit the noise and then all bets are off. We know that we can not measure infinite, but we mistakenly think that measuring zero is well within our measurement capability. However that is not the case. More accurately we try to measure the zero, more difficult it becomes. Actually in order to measure an "absolute zero" we can call "null", we need infinite capability. Clearly we need to come up with an alternative game plan if we have to overcome this limitation. 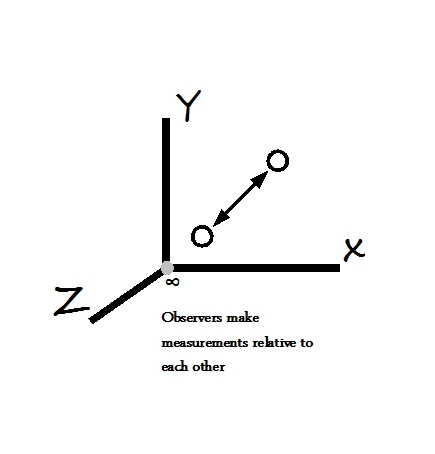 Notice that we have been talking in terms of the observer's capability. What we suggest we do is to move our description into a "capability" space. Therefore we replace conventional "zero" at the origin in the capability space by ∞. That done we run into another problem. How do we make measurements in a space which has ∞ at its origin? We resolve this situation by making measurements with respect to another observer with equal capability, who works as a reference for the observer making measurements. Thus we have effectively introduced a granularity in the measurement space because the observer making measurements has a limited capability. We are not done yet.  We further define our origin as
one of the observers. Now Observer-2 who
is making measurements has a very clear idea
about origin (Observer-1) and his measurements
are precise to the maximum of his own
capability. This
is the best we can do under the circumstances. We further define our origin as
one of the observers. Now Observer-2 who
is making measurements has a very clear idea
about origin (Observer-1) and his measurements
are precise to the maximum of his own
capability. This
is the best we can do under the circumstances.Thus the discrete nature of the measurement space is defined in terms of number of observers of equivalent capabilities. No prior existence of the origin or “zero” is assumed. The origin or “zero” and “infinite” are represented by the minimum and maximum of the observer's capability. Both “zero” and “infinite” will have different values for observers of different capabilities. 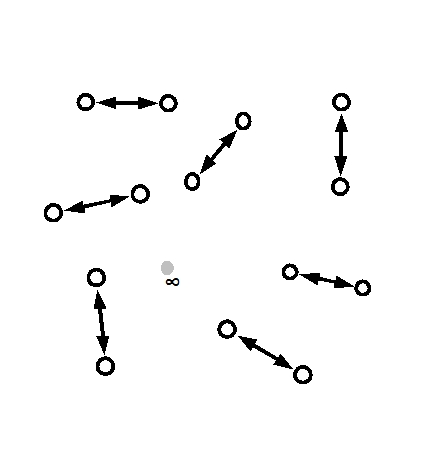 We will simplify our description further by
removing x, y, and z axes altogether. It
feels liberating now the axes are gone.
We will be essentially "counting" rather than
describing a phenomenon in terms of a
reference frame. The discrete
measurement space looks like a space in which
the measurements are kind of floating
around. Or are they really?
We will simplify our description further by
removing x, y, and z axes altogether. It
feels liberating now the axes are gone.
We will be essentially "counting" rather than
describing a phenomenon in terms of a
reference frame. The discrete
measurement space looks like a space in which
the measurements are kind of floating
around. Or are they really?
A minor but important detail we do not want
to miss, is that ∞ is
described by the gray region with no
boundary. This concept of boundary and
contents within will play a vital role in
our discussions much later.
Another important point we will like to mention is that by introducing a pair of identical observers, we have introduced the notion of symmetry in our discussion. Since this symmetry is based on the inability of the observer to measure the origin, this symmetry will be a fundamental symmetry in a discrete measurement space i.e. it can not broken by the resources available to the observers in discrete measurement space. Thus a discrete measurement space will have a symmetry by default. And if a symmetry exists then by Noether's theorem, a conserved current will exist. Therefore a discrete measurement space will have a dynamic characteristic. Also for every particle measured in the discrete measurement space we are likely to have at least one other particle of identical characteristics. Phew! It means that within our ignorance we are not alone. Let us call this symmetry a "virtual-twin" symmetry. We are sure that similar symmetry exists in literature, but until we understand physics better we just give it our own reference name. The virtual-twin or VT symmetry
in the discrete measurement space can not
be broken.
The shape of the ∞-region is not necessarily circular or spherical, but "indeterminate" as the observer can not accurately determine it. The observer can assume it to be of a symmetrical shape, but such symmetry will not be a measurement but an assumption. But right now we have to figure out what does the process of "counting" mean. We will have to develop an abacus for ourselves, to characterize the discrete measurement space.
 Information
on www.ijspace.org is licensed under a Creative Commons Attribution 4.0
International License.
|
"To a
place which has, no moon nor sun, no wind nor water, who will carry the message?" - Kabir, Sufi poet, 1440-1518. "Herein we may see a hint that not only the field concept, but also the space-time concept in small regions may require a fundamental modifications." - W. Pauli,General Principles of Quantum Mechanics, Springer-Verlag. |