28th June 2014
Earlier we had discussed the concept of an Infinite Fulcrum which essentially is a system with an infinite information source at the origin. The distance of a body from the fulcrum is in information space rather than the physical space as we know it.
 Let us consider the nature of the rotational motion in such system. We know that how a spinning skater spins faster in a more compact form, to conserve the angular momentum in classical mechanics. In a system of infinite fulcrum the effect will be quite opposite i.e. the extended form is likely to have higher rotational speed than the compact form. The objects at far distance from the fulcrum in this case will have higher velocity than those closer to the fulcrum. Which brings us to the relationship between rotational velocities and the distance from the center of spiral galaxies as measured by immortal Vera Cooper Rubin and W. Kent Ford Jr. for Andromeda Nebula.
Let us consider the nature of the rotational motion in such system. We know that how a spinning skater spins faster in a more compact form, to conserve the angular momentum in classical mechanics. In a system of infinite fulcrum the effect will be quite opposite i.e. the extended form is likely to have higher rotational speed than the compact form. The objects at far distance from the fulcrum in this case will have higher velocity than those closer to the fulcrum. Which brings us to the relationship between rotational velocities and the distance from the center of spiral galaxies as measured by immortal Vera Cooper Rubin and W. Kent Ford Jr. for Andromeda Nebula.
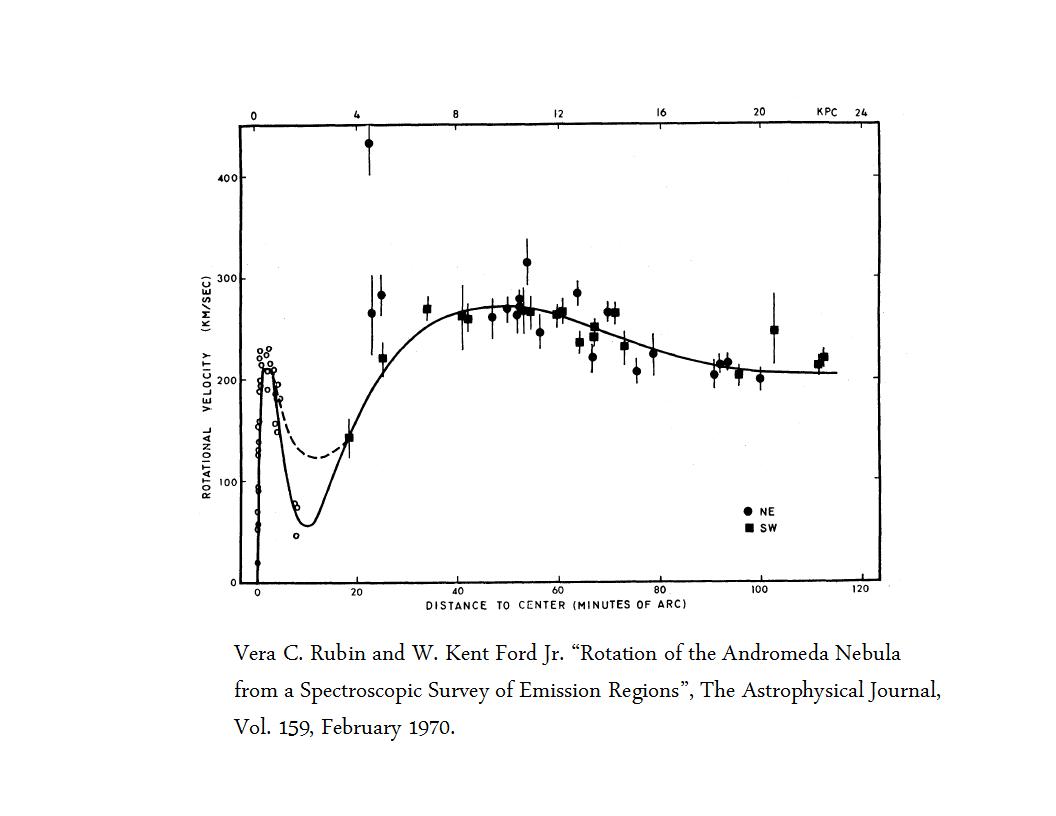
The pattern of the measured rotational speeds is quite opposite to what we expect from Newtonian mechanics. The rotational speed increases abruptly from zero than it seems to flatten out at large distances. This pattern is something we may expect from Infinite Fulcrum system. The rapid increase in the rotational speed represents structures with less and less information i.e. structures farther away from fulcrum. The structures spread out over a large physical distance are actually the structures confined within a very small region in the information space. These are what we may call QED structures and they effectively represent the limit of our observation capability. No wonder they all move with almost similar rotational velocities which are very high compared to those near the center of the galaxy. There are attempts being made to explain this observation based on the concept of dark-matter, which itself represents the portion of the information space we can not measure.


The pattern of the measured rotational speeds is quite opposite to what we expect from Newtonian mechanics. The rotational speed increases abruptly from zero than it seems to flatten out at large distances. This pattern is something we may expect from Infinite Fulcrum system. The rapid increase in the rotational speed represents structures with less and less information i.e. structures farther away from fulcrum. The structures spread out over a large physical distance are actually the structures confined within a very small region in the information space. These are what we may call QED structures and they effectively represent the limit of our observation capability. No wonder they all move with almost similar rotational velocities which are very high compared to those near the center of the galaxy. There are attempts being made to explain this observation based on the concept of dark-matter, which itself represents the portion of the information space we can not measure.

Information on www.ijspace.org is licensed under a Creative Commons Attribution 4.0 International License.
Previous Blogs:
Infinite Fulcrum
Cauchy and Gaussian Distributions
Discrete Space, b-field and lower mass bound
Incompleteness II
The supersymmetry
The cat in box
The initial state and symmetries
Incompleteness I
Discrete measurement space
The frog in well

