18th May 2014
In classical mechanics a lever works on the principle of balance of torque where the applied forces and their distances from the fulcrum, provide the relationship maintaining the equilibrium.
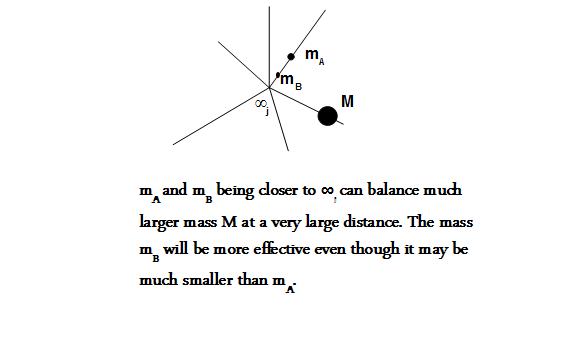
 Infinite fulcrum is a system with ∞j at the origin, the smaller mass being close to origin can balance a much larger mass at a very large distance from the origin. Let us call the mass in information space as i-mass. The smaller "i-mass", may be well below observation capability of a macroscopic observer in j-space. Closer the smaller i-mass is to the origin, higher is its capability in terms of balancing a much greater "i-mass" at a larger distance. The i-term mass is being used in a very generic manner to explain the concept in information space. It is not a quantity with units in kg.
Infinite fulcrum is a system with ∞j at the origin, the smaller mass being close to origin can balance a much larger mass at a very large distance from the origin. Let us call the mass in information space as i-mass. The smaller "i-mass", may be well below observation capability of a macroscopic observer in j-space. Closer the smaller i-mass is to the origin, higher is its capability in terms of balancing a much greater "i-mass" at a larger distance. The i-term mass is being used in a very generic manner to explain the concept in information space. It is not a quantity with units in kg.
 Theoretically an infinitesimal conventional mass in j-space, accurately placed at the origin can balance infinite conventional mass up to ∞j distance i.e. j-space itself. The capability to do so comes from <δi-∞j> source at i-j interface i.e. <t=0j> initial state.
Theoretically an infinitesimal conventional mass in j-space, accurately placed at the origin can balance infinite conventional mass up to ∞j distance i.e. j-space itself. The capability to do so comes from <δi-∞j> source at i-j interface i.e. <t=0j> initial state.
The measured mass may be for a single entity or a composite structure which itself may be represented as ∞'j in j-space where ∞'j << ∞j. The structures close to origin will contain lot more information than those away from the origin. Therefore these structures will be measured to be bound by much stronger force than those at large distance from the origin.
We can think of the situation in terms of handshakes. More information available firmer the handshake and consequently more energy is required to make a measurement. Some of the applications of the infinite fulcrum in fundamental structures are discussed below. We need to keep in mind that M, MA, and MB are the measured structures.
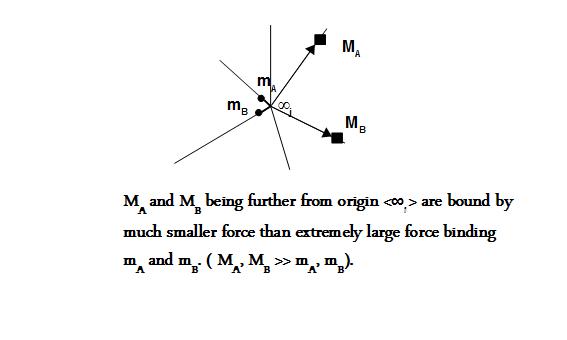
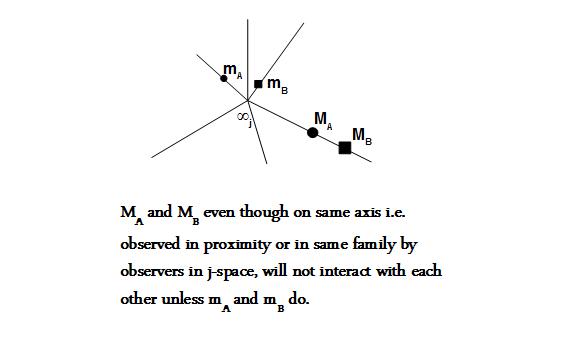



The measured mass may be for a single entity or a composite structure which itself may be represented as ∞'j in j-space where ∞'j << ∞j. The structures close to origin will contain lot more information than those away from the origin. Therefore these structures will be measured to be bound by much stronger force than those at large distance from the origin.
We can think of the situation in terms of handshakes. More information available firmer the handshake and consequently more energy is required to make a measurement. Some of the applications of the infinite fulcrum in fundamental structures are discussed below. We need to keep in mind that M, MA, and MB are the measured structures.



More than conventional three axes imply the existence of more information than what we can currently measure in 3-D.
The events corresponding to q = 1 value are virtually impossible to recreate, though under controlled environment, a temporary shift of the reference observer of observer pair in j-space towards origin <∞j> in j-space, can be accomplished. This will result in measurements of structures closer to q = 2 state, with more information content and very short life-time by the macroscopic observer ObsM before the equilibrium is restored. Larger the shift generated, larger will be the measured values such as the rest mass of these short life time structures.


Information on www.ijspace.org is licensed under a Creative Commons Attribution 4.0 International License.
Previous Blogs:
Cauchy and Gaussian Distributions
Discrete Space, b-field and lower mass bound
Incompleteness II
The supersymmetry
The cat in box
The initial state and symmetries
Incompleteness I
Discrete measurement space
The frog in well
