Home

         

Unknotting DNA 

 
6th April 2018


 































 

        In this blog we discuss the application of the knot theory in DNA structure. We will continue our discussions in Quantum Computing series afterwards.  We had earlier described the importance of the measurement capacity of a macroscopic observer in j-space and how it results in an Unknot (Shallow Well) and Trefoil knot (Box).  We next developed the description of a Trefoil knot in j-space.  The description was in form of Laurent polynomials and it satisfied the following properties:

• The structures for each knot-orientation were clearly distinguishable from each other.  Each polynomial representation was unique.
• Symmetries corresponding to Charge (state and anti-state, 'h'), Parity (reflection along an axis or the equivalently ACW or CW knot orientation) and Time (order of the crossings, 'h'), were addressed within the same polynomial.
• Chiral property could be distinguished.

The Trefoil knots represented the interaction as measured by the maximum efficiency observer Obsc (v~c).  The measurements made by the next most efficient observer is represented by the Figure-8 knot.  We explain further the description for the Figure-8 knot in j-space.  Afterwards we will discuss a rather interesting application of the knot theory in unknotting of DNA.

The knot diagram for the figure-8 knot, is shown as following:

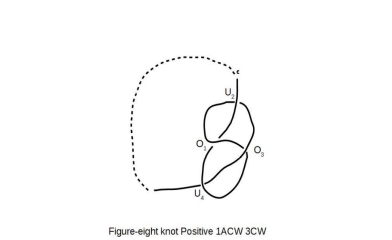
    The Figure-8 knot shown, begins with an Anticlockwise loop for the first crossing written as O1.  The following crossings U2, O3, and U4 are in Clockwise direction.  Hence the notation 1ACW3CW.  We call the knot Positive, as the first crossing is an over-crossing.

    The knot polynomial for the figure-8 knot can be written, in the manner similar to the one introduced for Trefoil knot earlier as following:

   As discussed earlier while drawing the Figure-8 knot, we noticed that the direction of sectional loops is Clockwise and Anticlockwise both with in the same knot.  In Trefoil knot the direction is exclusively either Clockwise and Anticlockwise. We therefore need to introduce a representation which along with the knot-polynomial, provides a complete picture to the observer by including the directions of sectional loops within a knot.  An example based on Figure-8 knot, is shown below:

    The knot description consists of the knot polynomial and representation columns.  For example (+, 1, 3) in above table, describes a knot whose first crossing is over-crossing (+).  One of its crossings, is the result of a loop with ACW orientation, whereas three of its crossings are result of loops with ACW orientation. 


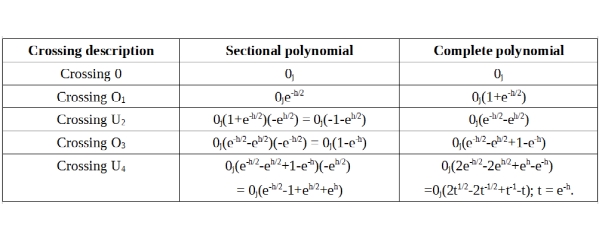
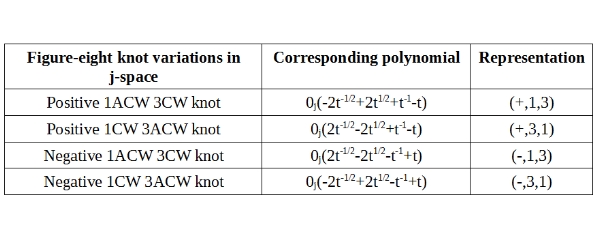
    If we compare the Trefoil and Figure-8 knots, we notice the absence of constant in the knot polynomial for Figure-8 knot.  The Trefoil knot in contrast has for example, a value "3" representing the contributions of 0j.  This is an important difference as the absence of the contribution of 0j in the knot polynomial for figure-8 knot, represents a corresponding physical structure, which has no memory of the initial state. 

    The structures with no memory of the initial state, are statistical in nature described by the random variables.  Thus if we write a knot polynomial which shows no contribution of 0j, then it is likely to be of statistical nature.  Such structures can be further reduced by a process similar to symmetry breaking, until contribution of 0j is accounted for, in the knot polynomials.  The most fundamental structure in j-space is represented by Trefoil knot, which has three alternating crossings, the required minimum, to form a stable knot.
 
    A fantastic application will be to apply j-space knot polynomials, to the mechanism used by enzymes to unpack DNAs for replication.  In j-space, enzymes and DNA both are observers, who are making measurements and being measured at the same time.  Each molecule in a DNA represents a measurement.  Subsequently by stringing together these measurements, a knot polynomial can be written for a specific DNA. 

    The DNA represented by knot polynomials with no contribution from 0j term, are more likely to be affected by enzymes and hence easy to replicate.  If the enzyme is related to a potentially catastrophic disease then such DNA are at risk.  Similarly the DNA represented by very high contributions of 0j term in their knot polynomials, are likely to be much more robust.


DNA and Enzymes
 
    Taking the argument further we can possibly also write similar knot polynomials for enzymes in j-space.  If we compare the knot polynomials written for enzymes and DNA, the enzymes corresponding to the polynomials of lower order (t-n, t+n) and with high contributions of 0j terms, are more likely to succeed in breaking down DNA with higher order polynomials which have small contributions of 0j terms. 

    In similar fashion, the DNA with lower order polynomials and with high contributions from 0j terms, should be immune to the effects of enzymes corresponding to higher order polynomials and with little contributions from 0j terms. 
 
Previous Blogs:
     




























 

                                                                                                                                                                                                                                   

Best viewed with Internet Explorer

Creative Commons License

Information on www.ijspace.org is licensed under a Creative Commons Attribution 4.0 International License.