logo
The Knot Formation in j-space     


Home

The Trefoil Knot

 

The objective is to develop an algebraic expression for knots, knots which are not further reducible in the discrete measurement space of an macroscopic observer ObsM, or j-space.  It should be fairly obvious that the permanent knots can only be formed when crossings are alternately over and under.  In this context, please also see the remark made by Professor Tait.  If two crossings are either consecutively over or consecutively under, then they are equivalent to an unknot and hence they can be removed from the knot diagram.
  

The requirement of the alternating crossings also has an important ramification.  The knots if they exist in a measurement space, represent the structures corresponding to a particle which can exist only in an excited quantum state. We can also say that the results derived from Knot-theory, correspond to the statistical and quantum-statistical measurement domains.


    The most elementary knot which can be formed with the requirement of the alternating over and under crossings, is the trefoil knot.  Next alternating knot, is the Figure-8 knot.  Let us assume that we can develop exact polynomials for trefoil and figure-8 knots both.  If a given more complex knot structure in j-space is converted into its irreducible form, and it turns out to be figure-8 knot rather than trefoil knot in j-space, then we know that there must exist at least one symmetry (Chiral symmetry for example).
 

This process is similar to saying that all the possible knots in j-space, must be embedded in the trefoil knot space.  We make similar statement in group theory, where we assert that most fundamental structure which can be measured,  is the convex structure, which is represented by zero-trace Pauli Spin matrices.  However in j-space knots, a convex structure is not possible as we are considering over- and under- crossings both.  We are likely to get a structure of the following form, instead of a zero-trace 2×2 matrix: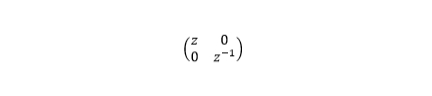

.

In this case the values of the exponents of the variables in the trace, should add up to zero.  If we look at the trace, we can identify Laurent Polynomials as possible description for knot structures in j-space.  In the following sections, we describe how to write polynomials in a discrete measurement space we call j-space, for a trefoil knot and its variations in terms of knot-orientation and reflection.


    We consider an exact source represented by an infinite information space where a string is formed of the measurements made by an observer of finite capacity, who is trying to determine the nature of the source.  In such case the entropy of the system will be continuously increasing and process as being measured, will be irreversible.  However since the observer has a finite capacity, the process as being measured is reversible but only within an infinitesimal 'h', defined by the observer's resources or its environment.  (Please note that an infinitesimal is represented by 'h' for illustrative purposes only.)

    Let us discuss, how prime knots will be formed in such space and how they will be represented algebraically.  To develop a description of a knot, the progress of measured information I in a discrete measurement space along the time-axis, is considered.  It can be described as in Eqn. 1,

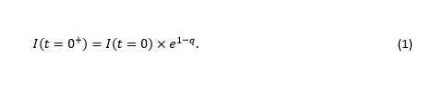In Equation 1, q is a natural number (q = 1, 2, 3 ...), I(t=0) represents the information available for the initial state (t = 0), and I(t = 0+) represents the information available at a later instant, (t = 0+).  A knot is formed when an observer cannot measure a state in a single measurement (single measurement represents zero entropy as loge1 = 0).  In this case more than one measurement is needed and the entropy comes into the picture.  We consider large q values where a statistical phenomenon is established.  In that case Eqn. 1, is modified to, 

We postulate, that a knot is formed and a polynomial is created, only when a measurement is made by a macroscopic observer ObsM.   A finite capacity observer (v << c) is always in a discrete measurement space.   If a state is below the observer's capacity threshold we define it as ɛ, where ɛ represents an indeterminate state for a finite capacity observer.   The knot formation in a discrete measurement space is shown in Fig. 1. 


Trefoil knot polynomials

    A trefoil knot as formed in a discrete measurement space for a given q-value, is shown in Fig. 2.  It is a 2-dimensional plane with third dimension representing the motion within an infinitesimal ‘h’ along the time-axis.  We have the following properties characterizing the knot,

   1. The motion along time-axis is in positive (over-crossing) and negative (under-crossing) directions both.  This motion is along the perpendicular to the plane of the page.

   2. The anticlockwise (ACW) or clockwise (CW) motions, are in the plane of the page.  They represent the orientation of the knot at each crossing.

   3. The order in which the crossing is approached is important.  For example in Fig. 2, U2 and O3 cannot occur before O1.  Similarly O3 cannot occur before U2.

   4. The nature of the first crossing defines the knot as positive or negative.  For example, if the first crossing of the knot is over-crossing (O1), the knot is classified as positive knot.  Similarly, if the first crossing of the knot is under-crossing (U1), the knot is classified as negative knot. 


 The polynomial for ACW positive trefoil knot is calculated as shown in Table-1. 

    In calculating the polynomial the ACW orientation,  is considered positive per trigonometric conventions.  A sectional polynomial, represents the contribution of the specific crossing, which is then added to the contributions from the previous sections.  The important part is the contribution of crossing 0.  It is written as 0j to emphasize that in j-space to measure absolute zero, infinite capacity is required.  Hence at best some minimum can be measured, which is represented as 0j.  During calculation of polynomial the inclusion of 0j plays an important role.  The polynomial is completed when a knot is formed.  We define the polynomial variable as t = e-h.  (Similar concept of knot thickening exists in conventional knot theory, except t in our case represents the absolute minimum distance an information string can shift along time-axis perpendicular to the 2D plane of the knot, in either direction.  It is important to note that in j-space we are discussing a topological space, instead of  the  geometrical or physical space.)  The polynomial for a positive ACW trefoil knot can be written from the Table-1 as, 

The normalized polynomial for a positive ACW trefoil knot is,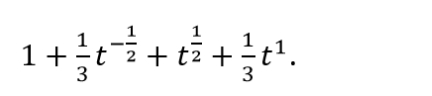

The coefficients of the polynomial take integer or fractional values.  The polynomial variable t represents the variation of the information within the quantum ‘h’.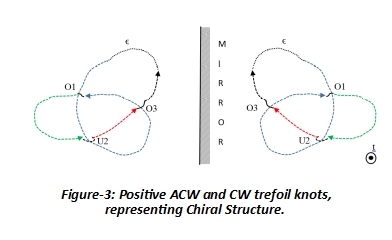

    We can next consider the reflection of positive ACW trefoil knot, which will be positive CW trefoil knot (Fig. 3).  In this case the orientation direction of the knot changes from ACW to CW, while the nature of over- and under-crossing and their respective order do not change.  The plane of reflection can be either vertical or horizontal.  In either case only change is in the orientation of the knot.  The calculation of polynomial in this case is shown in Table-2.  The CW orientation is negative per trigonometric convention. 

The polynomial for positive CW trefoil knot can be written as 3 - 3t1/2-t-1/2+ t where t = e-h.  We can similarly write the corresponding polynomials for negative ACW and CW knots.  The normalized polynomials for all four cases i.e. positive ACW,  positive CW,  negative ACW, and negative CW trefoil knots are summarized in the Table-3.

 

Additional Polynomials


    We can write a generalized algebraic expression for the normalized polynomials corresponding to the trefoil knot as in equation-3.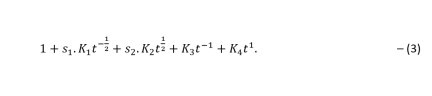

In eqn. 3, the coefficients (K1, K2, K3, K4) take the values (1/3, 1, 0, 1/3) for positive trefoil knot, and values (1, 1/3, 1/3, 0) for negative trefoil knot.  The coefficients s1 and s2 take the values (1, 1) and (-1, -1) for ACW and CW orientations of the trefoil knot.  We can write an additional set of the normalized polynomials for positive and negative trefoil knots for the values equal to (1, -1) and (-1, 1) for the coefficients (s1, s2) as shown in eqn. 4.  The values of the coefficients (K1, K2, K3, K4) are left unchanged.

We therefore have a set of eight normalized polynomials for a trefoil knot in a discrete measurement space.  The physical interpretation of the polynomials represented by eqn. 4, is yet to be ascertained.
 

Discussion

    For a trefoil knot four algebraic combinations are available, with the “alternating crossing” and the “order of crossing” constraints as shown in Table-3.  The structures are clearly distinguishable from each other as each polynomial representation is unique.  These polynomials have the characteristics of Laurent polynomials.  They can be thought of a state (positive trefoil knot), its anti-state (negative trefoil knot) and their respective reflections (CW and ACW).   We note that in order for a knot to form, over- and under-crossings must be alternated.  A minimum of three crossings (over- and under- combined) are required. 

     The 2-dimensional knot-orientation plane, is essentially 1-dimensional if the knot orientation values are taken to be +1 for ACW and -1 for CW, as we have done so far.  The polynomials which are of Laurent nature, are able to uniquely describe charge, parity and time symmetries.  The methodology described can be used to develop polynomials for higher order knot structures.  The description of the structure is in 2+1 dimensional plane.  The effect of entropy in the observer's environment is accounted for in j-space, by ensuring that:


(i) the crossings are ordered besides being alternate, and

(ii) time-axis exists and, an infinitesimal 'h' is defined in 1-dimensional plane along it, perpendicular to the plane of paper. 
 

    The infinitesimal 'h' represents the observer's capacity.  The physical description of a knot, for the observer making the measurements, is developed in the orientation plane which is 2-dimensional.  The 1-dimensional (time-axis) and 2-dimensional orientation plane for a knot are orthogonal to each other.

    Charge (positive-CW and negative-CW or positive-ACW & negative-ACW,  combined with 'h'), Parity (reflection along an axis or equivalently ACW or CW knot orientation) and Time (order of the crossings and 'h') symmetries are addressed within the same polynomial.  Chiral property can be distinguished, as the polynomials representing ACW and CW orientations for positive and negative knots, are unique. 

    The description in this case is 1+1 dimensional.  However we will require a 2-dimensional plane, because in a discrete measurement space while forming a knot, a finite capacity observer cannot retrace its path exactly, and therefore a loop is formed.   For example, an observer with lower capacity, is likely to form a much larger loop in the knot orientation plane compared to the loop formed by a higher capacity observer.   Therefore a 2-dimensional orientation plane is required for the comparison of the observers.  We will elaborate further in a later blog.

 

    Why do we want to write knot polynomials in discrete measurement space?  Because we as macroscopic observer ObsM, want to estimate the resources needed to extract information contained within a path AB for different observers, represented by a knot.  We know that different observers will measure different information from same path, hence different corresponding knot structures.  The lower capacity observer will extract less information and will take longer time,  hence the knot polynomial will be of higher order and more complicated.
 

    The most efficient macroscopic observer in j-space, is represented by the trefoil knot.  Which means that given a knot, if it can be proven to be embedded in trefoil knot space, is likely to provide maximum information using minimum resources (action).  Similarly if a knot is proven to be embedded in figure-eight knot space, then it will require a much higher amount of resources to provide the same amount of information.  We keep in mind that figure-eight knot is amphicheiral, whereas trefoil knot is not. 



 

updated 13th March 2018



















" It had for some time struck to me as very singular that, though I could easily prove that (when nugatory intersections are removed) a knot in which the crossings are alternately over and under is not further reducible ......"

- Professor Tait in Proceedings of the Royal Society of Edinburgh, 1876-77.