j-space knots

28^th November 2014

    The space-time metric has to obey the measurement-space topology and therefore if we know the topological properties, we can explain some of the most basic issues such as the definitions of Continuity and Connectedness. The description in terms of Energy and Momentum can follow afterwards.

    The knot theory is one of the instruments which allows us to visualize the possible topological states a system may take, over a period of time. What started as a suggestion by Lord Kelvin and consequently an extensive work done by Tait on characterizing the various types of knots, has evolved into a very powerful mathematical field which has the potential to unlock the fundamental principles guiding the formation of the elementary structures.

    Mathematically the knot structures are algebraically represented by knot-invariants, which are polynomials which remain unchanged for the equivalent knots. The earliest example of such polynomials is Alexander polynomial. The other well-known examples are Alexander-Conway polynomial, Jones polynomial, and HOMFLY polynomial. We must remember that these knot polynomials represent a description in three-dimensional space.

Conventionally we develop a mathematical structure for a physical knot based on certain mathematical rules, determine the knot invariants and correlate them to the probability amplitudes. A desirable quality of these knot-invariants is to make distinction between the knot-based on properties such as Chirality, as shown by Jones polynomial. Clearly more are the properties distinguished by a knot-invariant, more robust is the polynomial.

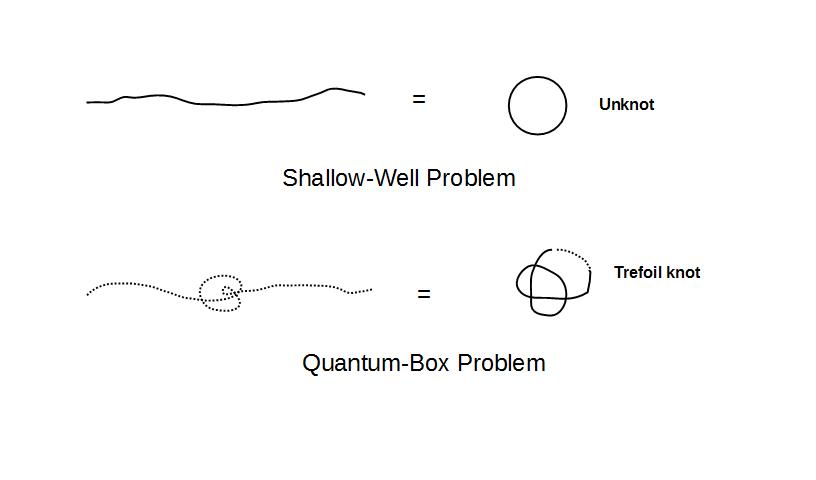
We can take a slightly different approach. Rather than assuming the existence of a knot, we form a knot made of step-by-step measurements in a space characterized by entropy. The time scale is extremely small of the order of Planck time. Also since the entropy is in picture, the order in which the moves are being made while forming the knot becomes important. The measurements are made by the macroscopic observer Obs_M. The knot polynomial is written in 2+1 dimensional measurement space instead of conventional R³ space.

For a given information-structure, an observer of very high capacity, Obs_c for example, will measure the structure as a shallow-well problem or a zero-entropy problem and hence an Unknot is formed. (A shallow potential well implies a single totally symmetric bound state. The measurement of this state, is not possible in the discrete measurement space or j-space.)

For the same information-structure and for an observer of infinitesimal capacity or Obs_M, the measurement is equivalent to an infinite well or Q-box problem. As a result the entropy is very high for Obs_M, and a knot is formed.

Therefore the nature of the knot is independent of the nature of the event and depends upon the observer's capacity. It is equivalent to saying that the poor man's black-hole is a rich man's pothole. The basic idea is shown below:

In the sections describing the formation of knots, we will discuss the formation of Trefoil knot in j-space. Later we will add sections on Figure-8 knot and Unknot. We will also consider the formation of composite knots as a result of the measurements made by a macroscopic observer Obs_M, and how they lead to higher order polynomials?

String Theory vs. Knot theory? It is reasonable to expect that the laws of nature will be metric independent, therefore perhaps we should sort out things in topological space first.

Information on www.ijspace.org is licensed under a Creative Commons Attribution 4.0 International License.