What Problems are we trying to solve?
21st February 2018
"But the theory was troubled. If
you tried to compute it more accurately, you
would find that the corrections you thought was
going to be small (the next term in the series,
for example) was in fact very large - in fact it
was infinity! So it turned out you
couldn't really compute anything beyond a
certain accuracy."
- Richard P. Feynman in
QED: The Strange Theory of Light and Matter.
"..But these changes in science are not made
wantonly, but carefully and cautiously by the best minds
and honest hearts, and not by any casual child who
thinks that the world may be changed as easily as
rolling off a log. "
- Lillian R. Lieber.
The idea behind Quantum
Computing initially, was to explore the
possibility of simulating physics using
computers. We were looking for exact
solutions to the problems in physics. In
real life there were some really interesting
problems which could not be solved using digital
computers in reasonable time frame and without
requiring excessive computational
resources. The applications for Quantum
Computing being actively researched into, are
encryption, reversible database search, machine
learning etc. Impressive
stuff, except it does not give us a sense of why
Quantum Computing should be considered a
disruptive technology?
For a technology to be
qualified as a disruptive technology, it has
to go into the mass production. The
invention of wheels and then their subsequent
use in vehicles can be considered example of a
disruptive technology from the early human
history. In modern world, personal
computers and smart-phones represent examples
of disruptive technologies. So far we do
not have any visibility on Quantum Computing
approaching masses in near future. It is
likely to stay as a high priced computational
device restricted to specialized domains.
However the Quantum Computing
is an extremely powerful concept,
which if and when realized has the potential
to transform the technological
landscape. Therefore it is a good
exercise to understand what problems other
than those known in physics and engineering,
exist and need to be solved.
Whether these problems will be solved by
the Quantum Computing or Topological
Computing, we do not know yet. These
problems are independent of any specific
knowledge domain and the path forward is
obscure at best. At a very high level,
we can state the following:
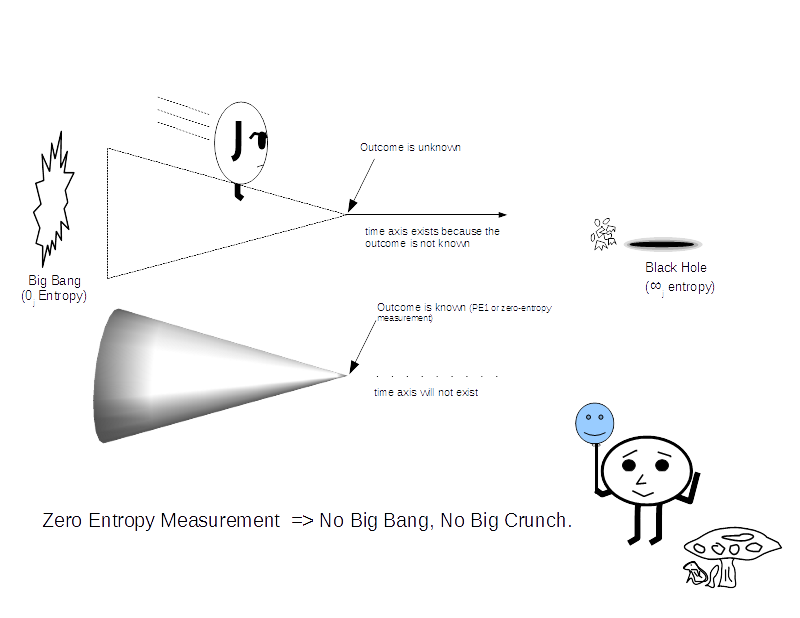
"The problem to be solved, is to
know or predict the outcome of the next
instant, with absolute precision in the
measurement space."
An observer who does not know this outcome, will
not know what to do or where to be next.
As a consequence the observer will stay in the
state of measurement. If we recall this
was the premise, based on
which the concept of the discrete measurement
space or j-space was developed.
The prediction of the
outcome of the next instant, is an extremely
difficult business.1
It can never be done in its entirety by a
macroscopic observer. However we have
some respite in the sense that when we speak
of a time-instant on the time-axis, we are
effectively within a stable environment
in the measurement metric of a macroscopic
observer, which is based on the
electron-photon interaction, as defined for
the q = 3 space. The information
to be measured can be enormous from a
macroscopic perspective, but it will always be
finite.
Once we have moved into the
q = 3 space, we have finite resources to
complete the objective stated above.2
Therefore the next level of the problem to be
solved within the human context, is the problem of
the resource optimization.3
The problem of resource
optimization manifests itself in many ways in
our daily lives. More intelligent the
solution, better the resource optimization and
less is the waste. Less waste means less
entropy. Therefore if we can achieve a
zero-entropy solution within q = 3 state, we
can perhaps solve the "impossible" problem.
Thus either Quantum or
Topological Computer must provide the
zero-entropy solution to a given
problem. Please note that a zero-entropy
solution is equal to the single measurement
(loge1 = 0)
solution. The zero-entropy solution
brings us to the requirement of a universal
computer capable of performing the reversible
computing, as identified earlier.
The Quantum Computing in its current state,
can not provide zero-entropy solutions.
That is why the Topological space and the
concepts associated with it, become very
important.
And then there is this small matter of finding the question, to which the answer is "42"....
1. To know the outcome of the next instant, is "impossible" business. If we already knew the outcome of the next instant, the measurements would not be needed to begin with.
2. In physics we have an equivalent concept known as "action": the resources available in a conservative system, to travel a path AB; or equivalently the resources available in a conservative system, to measure all the information contained within the path AB.
Previous Blogs:
Sigma-z and I
Spin Matrices
Rationale behind Irrational Numbers
The Ubiquitous z-Axis
Majorana
ZFC Axioms
Set Theory
Nutshell-2014
Knots in j-Space
Supercolliders
Force
Riemann Hypothesis
Andromeda Nebula
Infinite Fulcrum
Cauchy and Gaussian Distributions
Discrete Space, b-Field & Lower Mass Bound
Incompleteness II
The Supersymmetry
The Cat in Box
The Initial State and Symmetries
Incompleteness I
Discrete Measurement Space
The Frog in Well
Visual Complex Analysis
The Einstein Theory of Relativity
***
Attribution — You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. No additional restrictions — You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits. This is a human-readable summary of (and not a substitute for) the license.

