Entropy

The Entropy

Summary: We discuss the concepts of information, entropy, and observer's capacity in the discrete measurement space. We derive the propagation of information in discrete j-space. The q-values are introduced.

Definition

     The concept of entropy is probably one of the most profound ideas developed in physics, which has an enormous relevance in just about every aspect of our lives. It allows us to visualize the utilization of available resources to perform an action.

      We can consider a simple example. Suppose Aku is given $100 to purchase a text book by his mom. Now Aku goes and buys the book which costs him $50. Then on his way back he stops by to grab a pizza and soda for another $15. Then he spends another $10 on comics. Upon arriving back at home Aku returns remaining $25 to his mother.

      Now as far as Aku's mom is concerned the money spent on junk food and comics is not useful, therefore from her perspective the entropy is $15+$10 = $25. Our friend Aku thinks otherwise. He is not studious type and he did not like the text book he purchased. But for him the money spent on snacks and comics was worth it. So for Aku the entropy is $50 for the book plus $25 which he could not use, hence a total of $75.

    Notice the word "use". The entropy is observer dependent. The entropy tells us about the resources which can not be used for the assigned task due to inherent limitations of the system or the observer. The system for the macroscopic observer Obs_M (humans, v²/c² <<1), exists based on measurement made by Obs_c (v²/c²~1). Thus while in thermodynamic systems we may not notice the observer dependence, the value of the entropy for a macroscopic observer is dependent on the observer with maximum capacity to make precise measurements.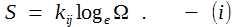

      We will use the concept of entropy in j-space and correlate the results obtained from measurements and the observer's capacity. Simply put if the observer Obs_j-1 measured a large number of states to complete a PE1_j result or event, than the entropy of the observer is high. If the observer Obs_j-2 measured a small number of states to complete the same PE1_j event then its entropy is low. The structure of the system represented by the observer Obs_j-2 will be more complex than that represented by Obs_j-1. Furthermore the observer Obs_j-1 will be in orbit of  Obs_j-2, as postulated.¹

      The information is a combination of multiple PE1_jevents. At the same time the observer's resources are fixed by the interval [0_j , ∞_j]. Therefore the larger the entropy less is the information an observer is likely to measure. The information is defined by the change in entropy. If we are reducing the entropy we are gaining more information. We can define entropy S as,

The Ω is number of measurements and k_ij is a constant characterizing the discrete measurement space or j-space. In thermodynamics k_ij is k_B known as the Boltzmann constant.  We will have to determine what is the significance of k_ij in measurement space. We will do it in a later section.

      Remember the discussion towards the end of Qbox section! We introduced δ_iin j-space.  The Obs_i measures all the information required for a PE1_j event in j-space due to δ_i, in one state. Hence the entropy in this case will be zero. At the same time δ_i really extends Obs_j capacity and as consequence the entropy for the same measurement is quite large for Obs_j. This is an important distinction we need to keep in mind.

      If an observer Obs_j is measuring same event, once by performing Ω_A measurements and then Ω_B measurements with improved efficiency such that Ω_A > Ω_B . The entropy for each case is S_A and S_B s.t. S_A > S_B. Then if we subtract information I_AB from low entropy state S_Bthen we get the high entropy state S_A . More the entropy less the information available to an observer.  Hence the information is also known as negentropy. The amount of information I_AB needed for efficiency improvement is,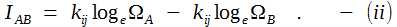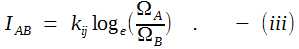

We can write equation (ii) as,

Thus we have information, entropy and resources. We use less resources if we have more information or less entropy or equivalently make less number of measurements to obtain the same result. A very obvious general rule of everyday life. The rule applies to nature as well.

Progress of Information in j-space

We consider now the progress of information from i-space into the discrete j-space as the information measured by the Q-box.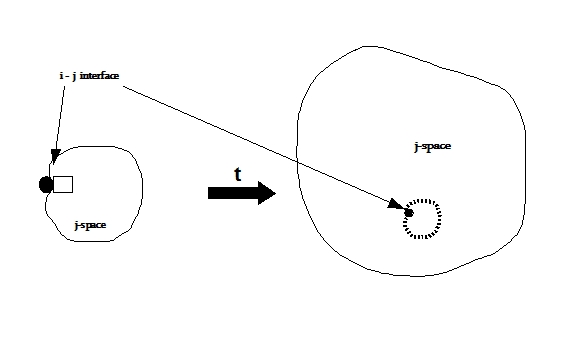

Keep in mind the expansion shown is within the Q-box, implying the location of true-point or source becomes more and more uncertain as the time progresses. Or the universe being measured is within the Q-box.

We note that the source, i-space, and the measurement space defining the observer environment, j-space, are separated. For the same source the environment of different observers and their measurements, will vary per capacity of the observers. Therefore it will be prudent to separate the concept of energy which is measured in j-space using Q-box and used to define thermodynamic properties, from the information received from the i-space or the source.

In discrete j-space the evolution from <t = 0_j> state on the time scale, due to increasing entropy, will degrade the information from its original value I(t = 0_j) to I(t = 0_j⁺) such that,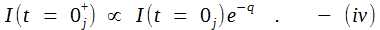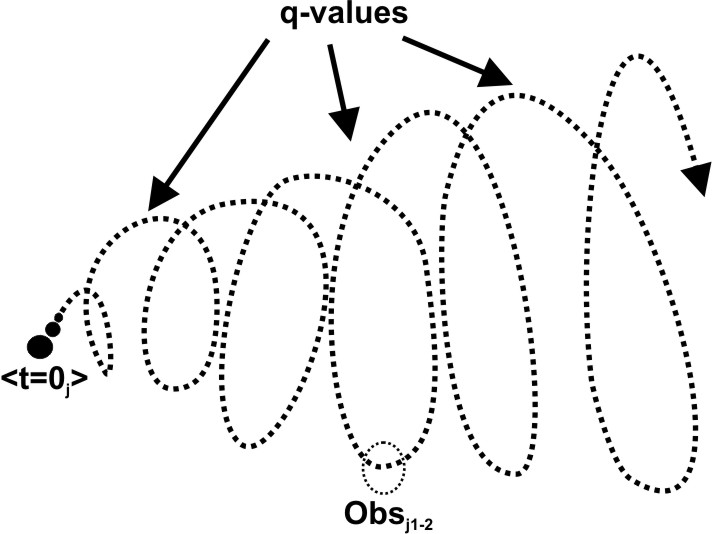

The instant (t = 0_j) represents the instant the measurements in j-space start and (t = 0_j⁺) represents the next instant at infinitesimal time interval. The exponential function is selected because its derivative is equal to itself and its initial value at q = 0 is 1. The variable q takes only the positive integral values in discrete measurement space. Each q-value represents a PE1_j event in discrete j-space. We can write equation (iv) as,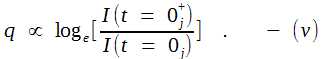

We need to remove the proportionality sign. To do that we determine the initial condition based on Obs_i measurements. For Obsi, the observer in i-space, all the outcomes are known and hence at the instant <t = 0j>,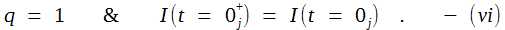

We have obtained the initial condition based on Obs_i capabilities. The initial conditions could not be determined precisely with Obs_j, the observer pair in discrete j-space, due to their inherent limitation in determining the origin with absolute accuracy. The variation of information in discrete j-space can be obtained from equation (v) as,

We can rewrite equation (vii) as,

The equation (viii), defines the relationship between the information at a later instant to the initial state information, in terms of PE1 measurements in a discrete measurement space or j-space. The relationship is independent of k_ij the constant characterizing the j-space. Please note that in deriving equation (viii), we have not considered any physical characteristics of the medium or the observer in j-space except for the observer's capacity to make measurements. The minimum value of q in discrete measurement space is 1.

Finally we have to consider what happens when the entropy for an observer is maximized i.e. at what point the observer can not make any more measurements. This part is straightforward. With increasing entropy the observer Obs_j is highly unlikely to complete a PE1_j measurement. The value of the information measured by the observer in j-space becomes 0_j for the observers in j-space at t = ∞_j-, where t = ∞_j- is the instant at which the entropy is maximized. The notation <∞j-> signifies an instant before the value on the time axis equals ∞_j or completion. No further information can be measured hence I(t = 0_j+) is null. The condition for this case can be written from equation (viii) as,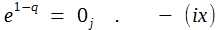

The 0_j in R.H.S. of above equation is measured as finite by the Obs_i, which means that the information I(t=∞_j^-) is finite, but Obs_j can not measure it as it is below his measurement capacity.

Before closing out this section, an explanation of the entropy relationship is necessary. When we wrote the equation (i), the logarithmic function is due to additive nature of entropy, which itself is due to the assumption of no interaction between the internal structures of the molecules. The conventional entropy S is defined for a thermodynamic system which in essence represents a macroscopic observer Obs_M with capacity v²/c² << 1. The assumption of the lack of interaction, corresponds to the absence of the information about <t = 0_j> or the initial state.

In j-space the assumption of non-interacting components is true for values of q approaching ∞j, but for low q values the interaction between states is much stronger and hence the contribution of interaction to entropy can not be ignored. The classic entropy defined by Boltzmann's H-theorem assumes no memory of the initial state and hence the ΔS ≥ 0 relationship is valid for the interacting macro-states (collisions), such as a system of ideal mono-atomic gas molecules. The calculations in this case use logarithmic relationship based on the classical picture. However in the case of the memory of the initial state being available, the process is not truly stochastic. The relationship ΔS ≥ 0 or positive entropy, is no longer necessary. In fact depending on the observer it could easily be ΔS < 0, which means that an observer with higher capacity (for e.g. Obs_i) is extracting more information from the same system than thought possible with capacity v²/c² ~ 1 (eg. electron-photon interaction).

Higher observer capacity or the condition ΔS < 0, represents the awareness of the initial state. The first step towards this awareness, will be the phenomenological explanation of the fine-structure constant. The phenomenological explanations require observer awareness of the initial state or <t = 0_j>.

Well, writing equations is good, everybody does it so did we. But then what is the connection to the nature? We shall discuss it next when we describe the fine-structure constant, Alpha.

______________

1. At this point we will state a basic principle without proof as:

"Every observer moves towards the state with maximum information, the observer can measure."

Please note the emphasis on "can measure". If a state with infinite information is available but the observer can not measure it then the observer can not move towards it, however the observer will stay in orbit. We can think of it in general terms as if information was wealth and if an observer knows about it (i.e. measure it) then the observer will move towards the state which provides the maximum wealth. We did not need physics to figure that part out. That is how the world we live in ticks.